Simulation von Klebstoffflüssen beim Verpressen

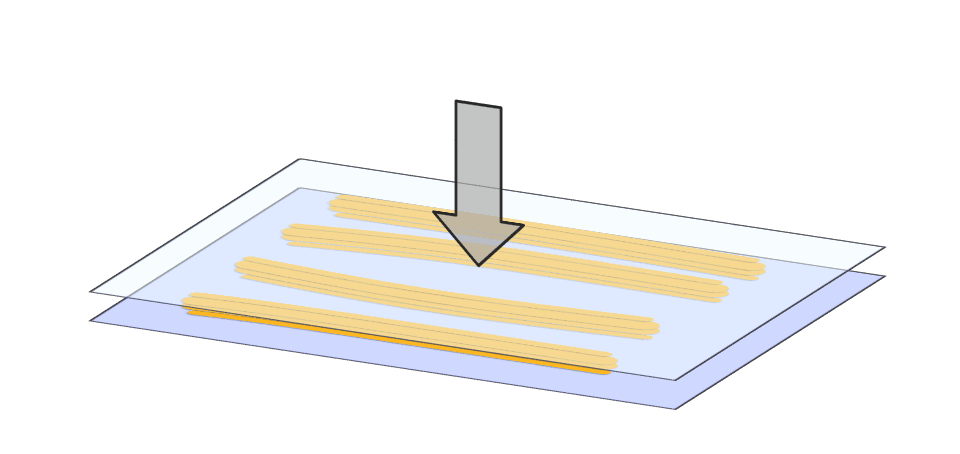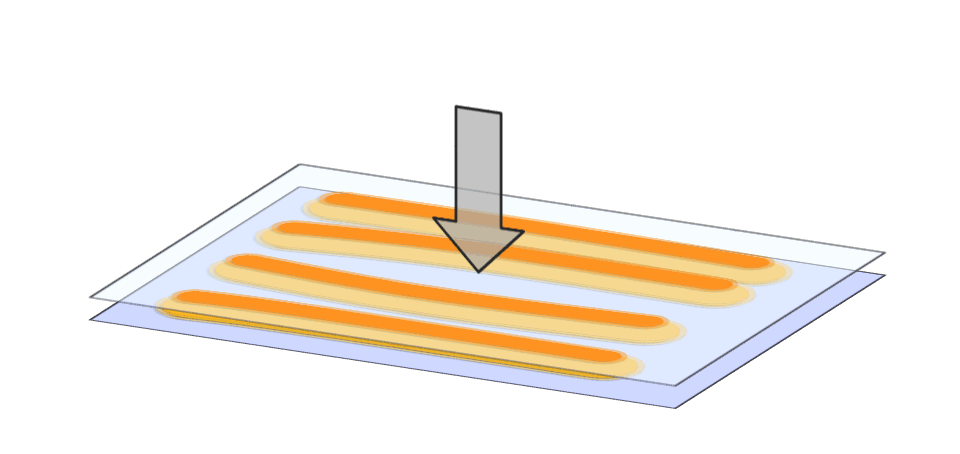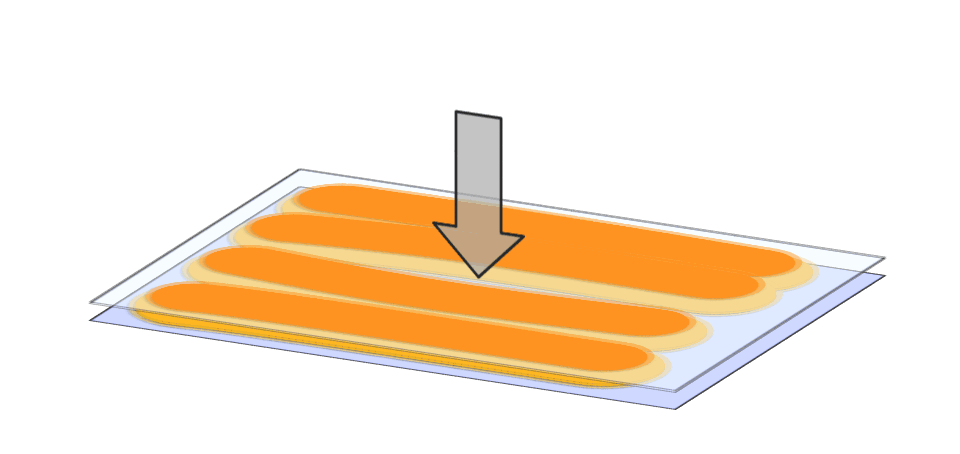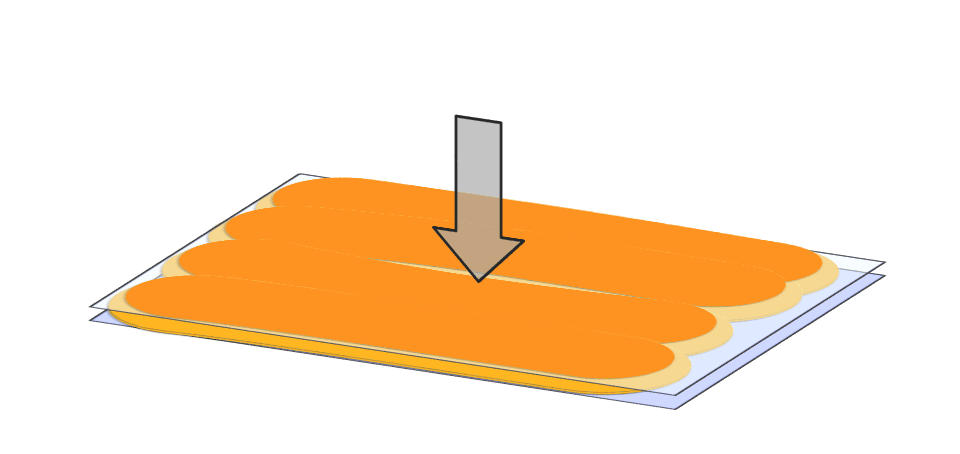
Schematische Darstellung - Ausbreitung von Auftragsraupen beim Verpressen

Effiziente Modelle zur Simulation der Strömung hochviskoser Kleb- und Dichtstoffe in Fertigungsprozessen

1. Forschungsziel

Resultierende Kraft über die Spalthöhe beim Verpressen - Vergleich Experiment und Simulation bei 3 Absinkgeschwindigkeiten - Serie A

Das erste Forschungsziel besteht darin, den Klebstofffluss im Fügespalt während des Verpressens effizient simulieren zu können. Konventionelle CFD-Simulationen stoßen hier häufig an ihre Grenzen. Grund dafür ist das große Aspektverhältnis von Auftragsfläche zu Fugendicke in Verbindung mit der Problematik der ständig nötigen Nachvernetzung.

Mit der Verwendung der sogenannten Reynolds-Gleichung greifen wir auf einen alternativen Ansatz zurück, der im Bereich der geschmierten Reibung bereits seit Jahren etabliert ist und in dem wir über langjährige Erfahrung verfügen [12]. In diesem Projekt übertragen wir die Mathematik der mangelgeschmierten Reibung auf die Klebstoffströmung [11] und haben bereits ausführlich gezeigt, dass wir diese Strömung sehr effizient und realitätsnah simulieren können [8,5]. Dabei können wir klebstoffspezifische Randbedingungen, wie Lufteinschlüsse [7] und nicht-newtonsches Materialverhalten [9] berücksichtigen.

Simulation einer Verpressung eines X-förmigen Auftragsmusters - 0,1mm pro Sekunde

Simulation einer Verpressung eines U-förmigen Auftragsmusters - 0,1mm pro Sekunde

Simulation einer Verpressung eines II-förmigen Auftragsmusters - 0,1mm pro Sekunde

2. Forschungsziel

Das zweite Forschungsziel besteht in der Entwicklung geeigneter Auftragsmuster, die eine vollständige Füllung der Klebefuge gewährleisten, ohne dass überschüssiger Klebstoff an den Rändern austritt. Hierzu haben wir 3 Strategien entwickelt:

Die erste Strategie basiert auf einem "Reverse Engineering"-Ansatz, bei dem wir die Zeitachse in der Simulation umkehren. Anstatt die Ausbreitung des Klebstoffs zu simulieren, untersuchen wir, wie der Klebstoff vor dem Verpressen verteilt war. [4]
Bei der zweiten Strategie verfolgen wir jedes Klebstoffteilchen und entfernen ausgetretene Teilchen in einem iterativen Prozess aus dem Auftragsmuster. [1]
Für die dritte Strategie nutzen wir künstliche neuronale Netze, die darauf trainiert sind, die optimale Anfangsverteilung für eine gegebene Endverteilung zu bestimmen. [2]

Abschließend haben wir experimentell nachgewiesen, dass die ermittelte optimale Klebstoffverteilung auch in der Praxis den Fügespalt optimal ausfüllt [3].

Optimales Auftragsmuster um ein Quadrat zu fuellen gefunden mit der Inversen Methode — Inverse Methode

Optimales Auftragsmuster um ein Quadrat zu fuellen gefunden mit der Iterativen Methode — Iterative Methode

Optimales Auftragsmuster um ein Quadrat zu fuellen gefunden mit der Neuronalen Netze Methode — Neuronale Netze Methode

Experimentell gefundenes Muster welches beim Zusammenpressen ein Rechteck ergibt — Experimentelle Methode

Zukünftige Forschungsziele

Für die Zukunft planen wir folgende Forschungsziele

Übertragung der Erkenntnisse vom Verpressen von Klebstoffen auf deren Injektion
Simulation des Verhaltens verschiedener Klebstoffe in einem Fügespalt (Stichwort Biadhesives)
Erforschung optimaler Auftragsmuster unter Berücksichtigung fertigungstechnischer Randbedingungen
Untersuchung optimaler Applikationsmuster unter Erweiterung für Hybridverbindungen (Kleben und Stanznieten)

Ausgewählte Publikationen

Scholtes K, Flaig F, Lehne F G, Kaufmann M, Fricke H, Vallée T. Müller M. Perfect application patterns for adhesive joints found by convolutional neural networks. In progress.
Kaufmann M, Flaig F, Müller M, Fricke H, Vallée T. Optimized adhesive application. International Journal of Adhesion and Adhesives 2024, p. 103620. https://doi.org/10.1016/j.ijadhadh.2024.103620
Flaig, F., Fräger, T., Kaufmann, M., Vallée, T., Fricke, H., & Müller, M. A practical strategy to identify appropriate application patterns for adhesively bonded joints. Proceedings in Applied Mathematics and Mechanics 2023; e202300080. https://doi.org/10.1002/pamm.202300080
Flaig F, Fräger T, Kaufmann M, Vallée T, Fricke H, Müller M. How to find the perfect application pattern for adhesively bonded joints? Journal of Advanced Joining Processes 2023;8:100147. https://doi.org/10.1016/j.jajp.2023.100147.
Kaufmann M, Flaig F, Müller M, Fricke H, Vallée T. How adhesives flow during joining. International Journal of Adhesion and Adhesives 2023;122:103315. https://doi.org/10.1016/j.ijadhadh.2022.103315.
Kaufmann M, Flaig F, Müller M, Fricke H, Vallée T. Do surface pretreatments for adhesives influence the squeeze flow? International Journal of Adhesion and Adhesives 2023:103362. https://doi.org/10.1016/j.ijadhadh.2023.103362.
Müller M, Willenbrock S, Stahl L, Vallée T, Fricke H. Towards the efficient modelling of trapped air pockets during squeeze flow. Exp. Comput. Multiph. Flow 2023(5):29–52. https://doi.org/10.1007/s42757-021-0125-3.
Kaufmann M, Flaig F, Müller M, Stahl L, Finke J, Vallée T et al. Experimental validation of a compression flow model of Non-Newtonian adhesives. The Journal of Adhesion 2022;98(14):2295–324. https://doi.org/10.1080/00218464.2021.1971081.
Müller M, Finke J, Stahl L, Tong Y, Fricke H, Vallée T. Development and validation of a compression flow model of non-Newtonian adhesives. The Journal of Adhesion 2022;98(9):1260–97. https://doi.org/10.1080/00218464.2021.1895771.
Müller, M; Tong, Y; Fricke, H; Vallée, T (2019): Transformation of tribological modelling of squeeze flows to simulate the flow of highly viscous adhesives and sealants in manufacturing processes. In: Proc. Appl. Math. Mech. 19 (1). https://doi.org/10.1002/pamm.201900056
Müller M, Tong Y, Fricke H, Vallée T. An efficient numerical model for the evaluation of compression flow of high-viscosity adhesives. International Journal of Adhesion and Adhesives 2018;85:251–62. https://doi.org/10.1016/j.ijadhadh.2018.05.023

Ausgewählte Publikationen zu Vorgängerprojekten

12. Müller, M; Ostermeyer, G-P; Bubser, F (2013): A contribution to the modeling of tribological processes under starved lubrication. In: Tribology International 64, S. 135–147. https://doi.org/10.1016/j.triboint.2013.03.011