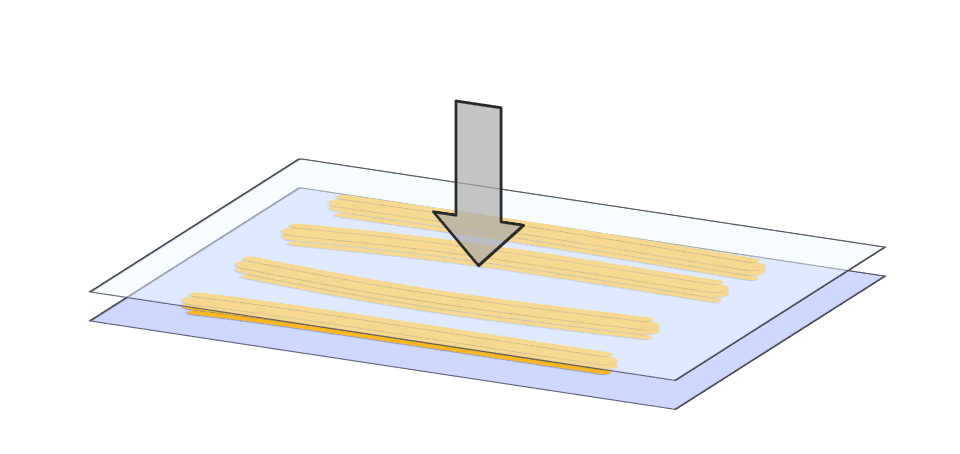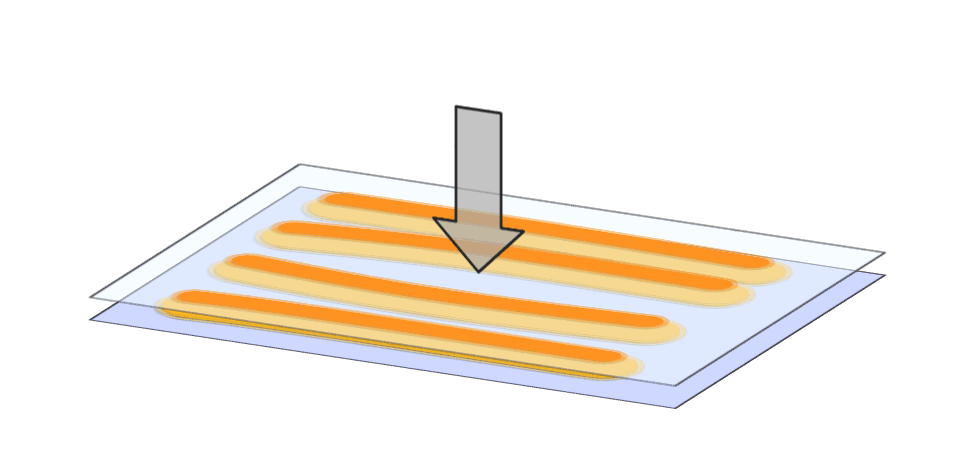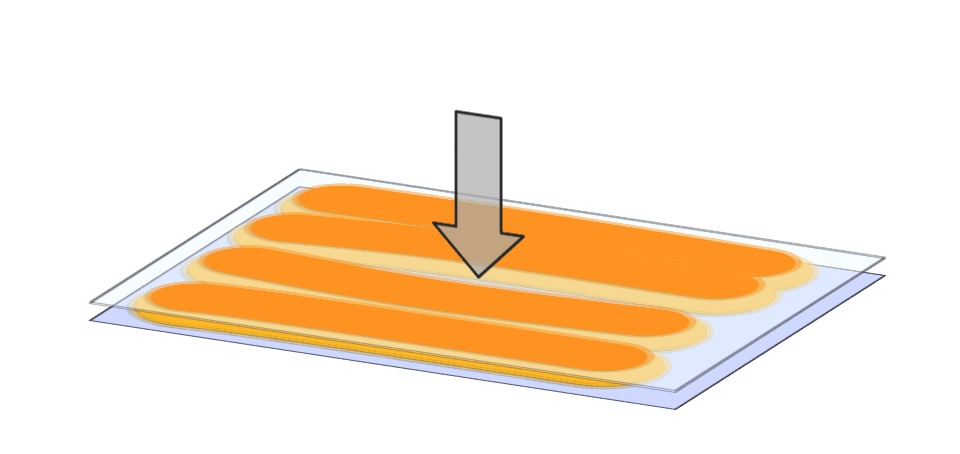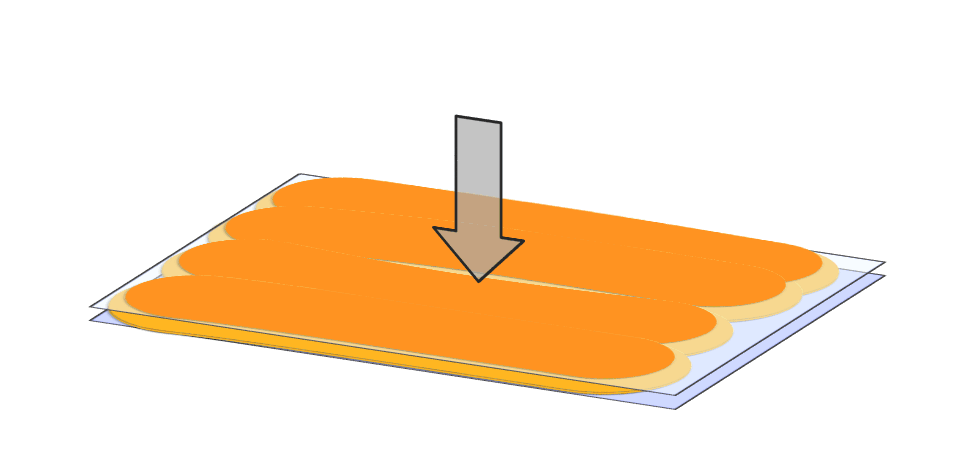
The first research objective is to be able to efficiently simulate the adhesive flow in joint gaps during pressing. Conventional CFD simulations often reach their limits here. The reason for this is the large aspect ratio of the application area to the joint thickness, combined with the problem of the constant need for remeshing.
By using the so-called Reynolds equation, we use an alternative approach that has been established for years in the field of lubricated friction and in which we have many years of experience [12]. In this project we transfer the mathematics of lubricated friction to adhesive flow [11] and have already shown in detail that we can simulate this flow very efficiently and realistically [8, 5]. There we can consider adhesive-specific boundary conditions such as air inclusions [7] and non-Newtonian material behaviour [9].
The second research objective is to develop suitable application patterns that ensure complete filling of the bonded joint without adhesive leakage at the edges. We have developed 3 strategies to achieve this:
Finally, we experimentally demonstrated that the optimal adhesive distribution determined also optimally fills the gap in practice [3].
Our research objectives for the future are
Scholtes K, Flaig F, Lehne F G, Kaufmann M, Fricke H, Vallée T. Müller M. Perfect application patterns for adhesive joints found by convolutional neural networks. In progress.
Kaufmann M, Flaig F, Müller M, Fricke H, Vallée T. Optimized adhesive application. International Journal of Adhesion and Adhesives 2024, p. 103620. https://doi.org/10.1016/j.ijadhadh.2024.103620
Flaig, F., Fräger, T., Kaufmann, M., Vallée, T., Fricke, H., & Müller, M. A practical strategy to identify appropriate application patterns for adhesively bonded joints. Proceedings in Applied Mathematics and Mechanics 2023; e202300080. https://doi.org/10.1002/pamm.202300080
Flaig F, Fräger T, Kaufmann M, Vallée T, Fricke H, Müller M. How to find the perfect application pattern for adhesively bonded joints? Journal of Advanced Joining Processes 2023;8:100147. https://doi.org/10.1016/j.jajp.2023.100147.
Kaufmann M, Flaig F, Müller M, Fricke H, Vallée T. How adhesives flow during joining. International Journal of Adhesion and Adhesives 2023;122:103315. https://doi.org/10.1016/j.ijadhadh.2022.103315.
Kaufmann M, Flaig F, Müller M, Fricke H, Vallée T. Do surface pretreatments for adhesives influence the squeeze flow? International Journal of Adhesion and Adhesives 2023:103362. https://doi.org/10.1016/j.ijadhadh.2023.103362.
Müller M, Willenbrock S, Stahl L, Vallée T, Fricke H. Towards the efficient modelling of trapped air pockets during squeeze flow. Exp. Comput. Multiph. Flow 2023(5):29–52. https://doi.org/10.1007/s42757-021-0125-3.
Kaufmann M, Flaig F, Müller M, Stahl L, Finke J, Vallée T et al. Experimental validation of a compression flow model of Non-Newtonian adhesives. The Journal of Adhesion 2022;98(14):2295–324. https://doi.org/10.1080/00218464.2021.1971081.
Müller M, Finke J, Stahl L, Tong Y, Fricke H, Vallée T. Development and validation of a compression flow model of non-Newtonian adhesives. The Journal of Adhesion 2022;98(9):1260–97. https://doi.org/10.1080/00218464.2021.1895771.
Müller, M; Tong, Y; Fricke, H; Vallée, T (2019): Transformation of tribological modelling of squeeze flows to simulate the flow of highly viscous adhesives and sealants in manufacturing processes. In: Proc. Appl. Math. Mech. 19 (1). https://doi.org/10.1002/pamm.201900056
Müller M, Tong Y, Fricke H, Vallée T. An efficient numerical model for the evaluation of compression flow of high-viscosity adhesives. International Journal of Adhesion and Adhesives 2018;85:251–62. https://doi.org/10.1016/j.ijadhadh.2018.05.023
12. Müller, M; Ostermeyer, G-P; Bubser, F (2013): A contribution to the modeling of tribological processes under starved lubrication. In: Tribology International 64, S. 135–147. https://doi.org/10.1016/j.triboint.2013.03.011
